Counting Squares

NPR's "Science Friday" posted a square-counting puzzle on their Facebook page yesterday, and a friend of mine challenged me to write a program to count them, hopefully coming up with the same answer (40) that we did with a manual count.

My first pass is a generalized (more or less) solution where different sized boards can be created with arbitrary horizontal or vertical lines. It's not the most solid thing I've ever written, doesn't take user inputs or validate the hardcoded input, but it illustrates a simple, brute-force attack of the problem.

This requires an HTML5-capable browser (Chrome, Firefox, Safari), and should start counting 5 seconds after loading.

(Read more)

Dear Scout

So Scout's father moved to California, and this weekend I flew her out to see him, where she'll stay until just before school starts. Combine missing a girl I love with my recent dive into cryptography, and the natural outcome is, of course, to write her a letter - in secret code!

When I was in high school, I had the idea to write a substitution cipher using symbols for letters. My code consisted of squares, circles, triangles, stars, horizontal, vertical, and diagonal lines, plus and equals signs, and some other unique but easy to draw symbols that the intervening 25 years has wiped from my memory. I used it to write a letter of no particular consequence to my friend Rachel (actually she was my friend Bill's friend, who I poached for purposes of odd geeky stuff like inventing strategy games to play and reviewing her early short stories), and she decoded it with little effort, predictable given her intelligence. What made it pretty straightforward to decode was context. I had formatted the letter like a letter, complete with spaces between words, and the encoded greeting "Dear Rachel" which let her immediately translate the 7 letters a, c, d, e, h, l, and r. Since "a" was included, a lone "I" was easy to translate, and then the rest could be filled in with a style akin to Sudoku, filling in words that were mostly complete already, and adding the newly translated letters to other words.

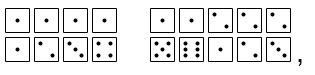
I wanted to do something like that for Scout, but I thought of a symbol set that would be both easy to write a program for, and comprise 26 letters and 10 digits: pairs of dice. Each die face could have a value of 1 through 6, giving 36 possibilities for a pair. I didn't want the code to be as easy as iterating through the alphabet and replacing 1.1 with a, 1.2 with b, etc., but at the same time I didn't want it to be so complex as to be off-putting for a 7 year old. It eventually ocurred to me that "Dear Scout" was an even better greeting than Rachel's, as it had no overlapping letters. If I kept the cipher alphabetized, but pulled "Dear Scout" to the beginning of the cipher, then the greeting would look like this:

(Read more)

Encryption, part 2: Elgamal and the Discrete Logarithm

In my quest to better understand the mechanics of encryption, I've found the Elgamal method the hardest to get my head around. The problem was not that the underlying math is difficult, it was that I didn't know some of the background terminology (cyclic group, congruence class, group isomorphism), the various explanations online all used different variables, and made references to "mathy" things it was supposed the reader was already familiar with. Lastly, the articles on discrete logs and Elgamal encryption on my go-to site for techie info, Wikipedia, were a hot mess, mistaking modular multiplicative inverse for division, and leaving out crucial middle steps (how to get from "collect underpants" to "profit", as it were). The whole affair really shook my faith in using Wikipedia as a trusted source for tech info.

A relatively simple explanation is this: You and your buddy both have a secret that combines to form an encryption key. To encrypt a message, multiply the key by the message value, divide by a modulus, and the remainder is your ciphertext. To decrypt, multiply the ciphertext by the key's inverse, and, again, divide by the modulus, and the remainder is the original message. Fin.

There is, naturally, some math involved, most of it geared around how to build the secret key so only you and your buddy know it, without either of you revealing your part of the secret. Let's start with some of the basic terminology, then get into the mechanics of building the encryption key.

(Read more)